Trie (Keyword Tree) Prefix Tree
Strings can essentially be viewed as the most important and common topics for a variety of programming problems. String processing has a…
Strings can essentially be viewed as the most important and common topics for a variety of programming problems. String processing has a variety of real-world applications too, such as:
Search Engines
Genome Analysis
Data Analytics
All the content presented to us in textual form can be visualized as nothing but just strings.
Tries:
Tries are an extremely special and useful data-structure that is based on the prefix of a string. They are used to represent the “Retrieval” of data and thus the name Trie.
Prefix: What is the prefix:
The prefix of a string is nothing but any n letters n≤|S| that can be considered beginning strictly from the starting of a string. For example, the word “abacaba” has the following prefixes:
a
ab
aba
abac
abaca
abacab
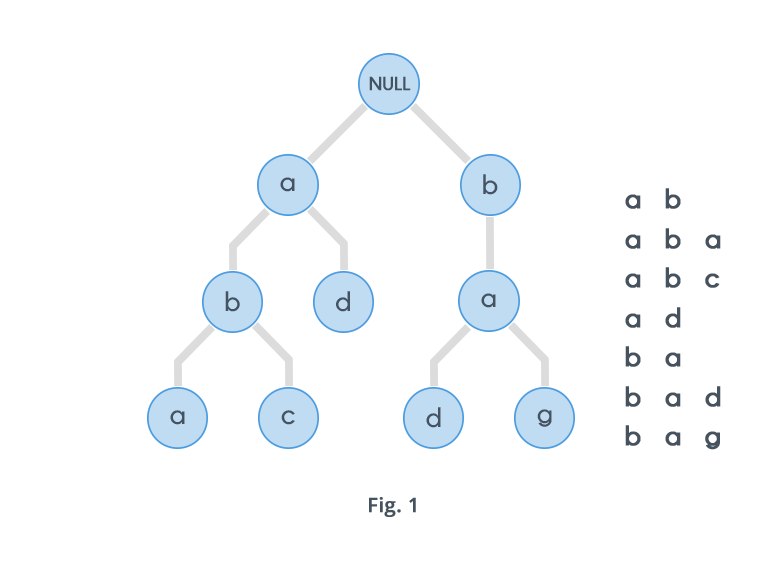
A Trie is a special data structure used to store strings that can be visualized like a graph. It consists of nodes and edges. Each node consists of at max 26 children and edges connect each parent node to its children. These 26 pointers are nothing but pointers for each of the 26 letters of the English alphabet A separate edge is maintained for every edge.
Strings are stored in a top to bottom manner on the basis of their prefix in a trie. All prefixes of length 1 are stored until level 1, all prefixes of length 2 are sorted until level 2, and so on.
For example, consider the following diagram :
Applications
As a replacement for other data structures
As discussed below, a trie has a number of advantages over binary search trees.
A Trie can also be used to replace a hash table, over which it has the following advantages:
Looking up data in a trie is faster in the worst case, O(m) time (where m is the length of a search string), compared to an imperfect hash table. An imperfect hash table can have key collisions. A key collision is the hash function mapping of different keys to the same position in a hash table. The worst-case lookup speed in an imperfect hash table is O(N) time, but far more typically is O(1), with O(m) time spent evaluating the hash.
There are no collisions of different keys in a trie.
Buckets in a trie, which are analogous to hash table buckets that store key collisions, are necessary only if a single key is associated with more than one value.
There is no need to provide a hash function or to change hash functions as more keys are added to a trie.
A trie can provide an alphabetical ordering of the entries by key.
However, a trie also has some drawbacks compared to a hash table:
Trie lookup can be slower than hash table lookup, especially if the data is directly accessed on a hard disk drive or some other secondary storage device where the random-access time is high compared to main memory.
Some keys, such as floating-point numbers, can lead to long chains and prefixes that are not particularly meaningful. Nevertheless, a bitwise trie can handle standard IEEE single and double format floating-point numbers.
Some tries can require more space than a hash table, as memory may be allocated for each character in the search string, rather than a single chunk of memory for the whole entry, as in most hash tables.
Dictionary representation
A common application of a trie is storing a predictive text or autocomplete dictionary, such as found on a mobile telephone. Such applications take advantage of a trie’s ability to quickly search for, insert, and delete entries; however, if storing dictionary words is all that is required (i.e., storage of information auxiliary to each word is not required), a minimal deterministic acyclic finite state automaton (DAFSA) would use less space than a trie. This is because a DAFSA can compress identical branches from the trie which correspond to the same suffixes (or parts) of different words being stored.
Tries are also well suited for implementing approximate matching algorithms, including those used in spell checking and hyphenation software.
Term indexing
A discrimination tree term index stores its information in a trie data structure.
Algorithms
The trie is a tree of nodes that supports Find and Insert operations. Find returns the value for a key string, and Insert inserts a string (the key) and a value into the trie. Both Insert and Find run in O(m) time, where m is the length of the key.
A simple Node class can be used to represent nodes in the trie:
class Node:
def __init__(self) -> None:
# Note that using dictionary for children (as in this implementation)
# would not allow lexicographic sorting mentioned in the next section
# (Sorting), because an ordinary dictionary would not preserve the
# order of the keys
self.children: Dict[str, Node] = {} # mapping from character ==> Node
self.value: Any = NoneNote that children is a dictionary of characters to a node's children; and it is said that a "terminal" node is one that represents a complete string.
A trie's value can be looked up as follows:
def find(node: Node, key: str) -> Any:
"""Find value by key in node."""
for char in key:
if char in node.children:
node = node.children[char]
else:
return None
return node.valueSlight modifications of this routine can be utilized
to check if there is any word in the trie that starts with a given prefix, and
to return the deepest node corresponding to some prefix of a given string.
Insertion proceeds by walking the trie according to the string to be inserted, then appending new nodes for the suffix of the string that is not contained in the trie:
def insert(node: Node, key: str, value: Any) -> None:
"""Insert key/value pair into node."""
for char in key:
if char not in node.children:
node.children[char] = Node()
node = node.children[char]
node.value = valueKotlin Implementation of Trie :
The basic concept of the Trie is every node can have a maximum of 26 child as we have 26 alphabets [a-z].
So we have to use Node with a HashMap that will store characters as Key and values as Node.
Insert in Trie :
So we will add character by character in Trie, if we current node’s map contains the same character then we can move forward otherwise we will create a Node.
If All characters has inserted then marked that Node as isWorldend .
Search in Trie :
We can search as we do in the insert, search char by char in Trie until we our character is finished then check isWorldEnd is true then return true else false.
Search Prefix in Trie :
Searching Prefix is the same like Search a Keyword, the only difference is that we can ignore isWorldEnd value as if all characters match return true.
Below is the code for Trie :
class Trie {
private val root = Node(0.toChar())
inner class Node(val char: Char) {
val map = HashMap<Char, Node>()
var isWorldEnd = false
}
fun insert(word: String) {
if (word.isNotEmpty()) {
insertNode(root,word,0)
}
}
private fun insertNode(node: Node, word: String, i: Int) {
val index = i
if (index < word.length) {
val char = word.elementAt(i)
if (node.map.containsKey(char)) {
val child = node.map[char]
insertNode(child!!,word,index+1)
} else {
node.map[char] = Node(char)
insertNode(node.map[char]!!,word,index+1)
}
}
else{
node.isWorldEnd = true
}
}
/** Returns if the word is in the trie. */
fun search(word: String): Boolean {
if(word.isNotEmpty()){
var index = 0
var node = root
while (index < word.length){
val char = word.elementAt(index)
if(node.map.containsKey(char)){
node = node.map[char]!!
index++
}
else{
return false
}
}
if(node.isWorldEnd){
return true
}
}
return false
}
private fun searchPrefix(word: String) : Boolean{
if(word.isNotEmpty()){
var index = 0
var node = root
while (index < word.length){
val char = word.elementAt(index)
if(node.map.containsKey(char)){
node = node.map[char]!!
index++
}
else{
return false
}
}
}
return true
}
/** Returns if there is any word in the trie that starts with the given prefix. */
fun startsWith(prefix: String): Boolean {
return searchPrefix(prefix)
}
}Thanks for reading this , Please like and subscribe .